Разбираем основные свойства и формулы геометрической прогрессии, строим графики и решаем задачи.
Представьте, что у вас есть пробирка с бактериями, которые делятся каждые два часа. Предположим, в самом начале их было всего 10, а рост бактерий будет происходить так:
- Начальная популяция: 10 бактерий.
- Через два часа: 10 × 2 = 20 бактерий.
- Через четыре часа: 20 × 2 = 40 бактерий.
- Через шесть часов: 40 × 2 = 80 бактерий.
Каждые два часа популяция бактерий увеличивается в два раза. Это и есть проявление геометрической прогрессии. Дадим ей определение.
В этой статье разберёмся, как устроена геометрическая прогрессия, для чего она нужна и почему числа в ней так быстро увеличиваются. В конце статьи вас ждут практические задачки, которые помогут закрепить материал.
Формулы геометрической прогрессии
Разберём основные формулы геометрической прогрессии.
Формула общего члена
С помощью формулы общего члена прогрессии можно найти любой член прогрессии, зная только первый член и знаменатель. Например, так можно узнать, сколько бактерий будет в пробирке через сутки, если они делятся каждые два часа.
В общем виде формула выглядит так:
an = a1 × qn−1
В ней:
- an — n-й член прогрессии.
- a1 — первый член прогрессии.
- q — знаменатель (коэффициент) прогрессии, который определяет разницу между двумя соседними членами прогрессии.
- n — номер члена.
Вернёмся к нашим бактериям и посчитаем, сколько их будет в пробирке через сутки. В этом случае первым членом прогрессии будет начальное число бактерий, а знаменателем — количество часов, которое нужно им для деления:
an = 10 × 2n−1
Бактерии делятся каждые два часа, в сутках будет 12 интервалов деления. Нас интересует 13-й член прогрессии:
a13 = 10 × 212 = 10 × 4096 = 40 960
Таким образом, через сутки у нас будет 40 960 бактерий.
Геометрическая прогрессия может быть как возрастающей, так и убывающей. Если знаменатель q > 1, то прогрессия возрастающая, так как каждый её последующий член больше предыдущего. Если q < 1, то прогрессия будет убывать.
— возрастающая прогрессия.
— убывающая прогрессия.
Сумма первых n членов геометрической прогрессии
Как посчитать сумму нескольких членов прогрессии? Самый простой вариант — просто найти эти члены и сложить. Такой подход применим только для небольших прогрессий. Представьте, что у вас несколько десятков слагаемых. На нахождение их суммы с помощью обычного сложения уйдёт очень много времени.
Можно облегчить себе задачу и воспользоваться формулой суммы первых членов прогрессии:
В ней:
- Sn — сумма первых n членов прогрессии.
- a1 — первый член прогрессии.
- q — знаменатель прогрессии.
- n — количество членов, сумму которых нужно найти.
Важно отметить, что формула выше актуальна только в случае, когда знаменатель прогрессии не равен единице (q ≠ 1). Если q = 1, то сумма первых n членовнаходится следующим образом:
Sn = n ⋅ a1
Характеристическое свойство геометрической прогрессии
В геометрической прогрессии квадрат любого числа всегда равен произведению его соседних членов. Это свойство называют характеристическим. С его помощью можно проверить, является ли последовательность чисел геометрической прогрессией.
Исходя из этого можно возвести в квадрат второй член прогрессии и перемножить между собой первый и третий член прогрессии. По характеристическому свойству должны получиться одинаковые числа:
Бесконечно убывающая геометрическая прогрессия
В убывающей геометрической прогрессии, где ∣q∣ < 1, члены прогрессии становятся всё меньше и меньше. Но мы всё равно можем найти их сумму по следующей формуле:
В ней:
- S∞ — сумма бесконечно многих членов прогрессии.
- a1 — первый член прогрессии.
- q — знаменатель прогрессии, где ∣q∣ < 1.
График членов геометрической прогрессии
Рассмотрим, как располагаются члены прогрессии в двумерной системе координат. Пусть на горизонтальной оси X будут размещаться номера членов прогрессии n, а на вертикальной оси Y — значения этих членов an. Тогда графиком прогрессии будет показательная функция.
Графики геометрических прогрессий растут или убывают в зависимости от знака знаменателя q:
- Если q > 1: график представляет собой экспоненциальный рост, члены прогрессии увеличиваются, и кривая растёт вверх.
- Если q < 0: график будет колебаться вверх и вниз в зависимости от чётности или нечётности номера члена.
Рассмотрим прогрессию 3, 6, 12, 24, …, 3 × 2n−1.
Отложим на оси X номера членов прогрессии n, а на оси Y — значения этих членов an. В этом случае члены геометрической прогрессии будут располагаться на графике функции:
y = 3 × 2x−1
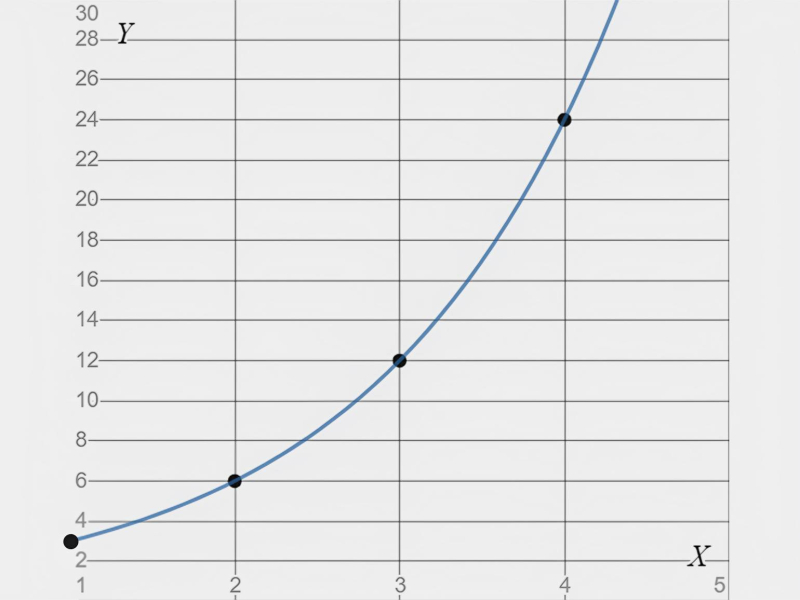
Изображение: Skillbox Media
- Если 0 < q < 1: график представляет собой экспоненциальное убывание. Члены прогрессии уменьшаются. Кривая будет стремиться к нулю, но никогда не достигнет его.
Рассмотрим убывающую прогрессию:
Если будем откладывать на оси X номера членов прогрессии n, а на оси Y — значения an, то члены геометрической прогрессии будут располагаться на графике функции:
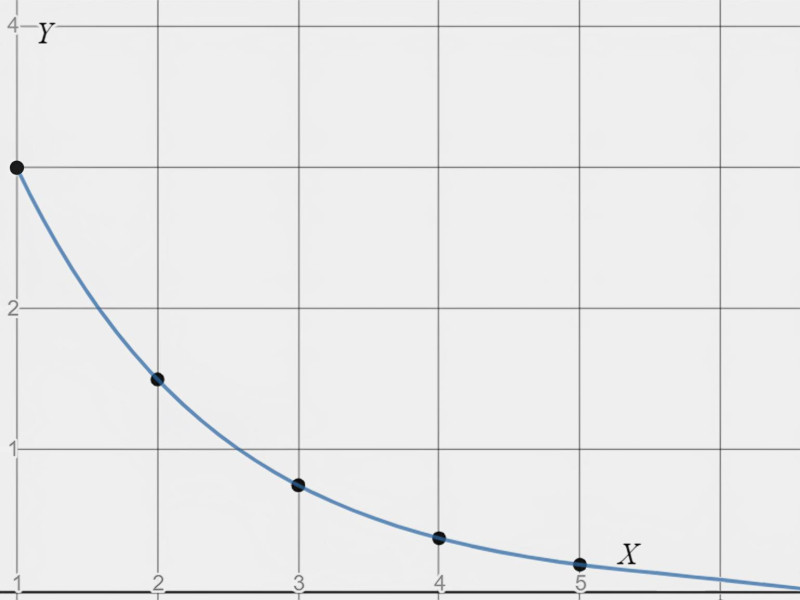
Изображение: Skillbox Media
Практические задачи
Теперь мы знаем все формулы и свойства геометрической прогрессии, которые могут пригодиться для решения практических задач. Ниже представлены три задачи и подробные решения. Не спешите смотреть ответ, сначала попробуйте решить сами.
Задача 1
Первый член геометрической прогрессии a1 = 3, знаменатель q = 2. Найдите третий и четвёртый член прогрессии.
Формула n-го члена прогрессии выглядит так:
an = a1 × qn−1
Используем её для нахождения a3 и a4. Для этого просто подставим значения и посчитаем.
Найдём третий член (a3):
a3 = 3 × 23−1 = 3 × 22 = 3 × 4 = 12
Теперь посчитаем четвёртый член (a4):
a4 = 3 × 24−1 = 3 × 23 = 3 × 8 = 24
Задача 2
Найдите сумму первых пяти членов геометрической прогрессии, если a1 = 1, а знаменатель q = 3.
Формула суммы первых n членов геометрической прогрессии выглядит так:
Подставим в неё значения из условий задачи:
Задача 3
Является ли последовательность чисел 2, 6, 19, 57, 172 геометрической прогрессией?
На первый взгляд кажется, что числа в последовательности 2, 6, 19, 57, 172 увеличиваются быстро, как в геометрической прогрессии. Но проверим их с помощью характеристического свойства.
Возведём в квадрат второй член прогрессии a2 = 6 и умножим первый член a1 = 2 на третий a3 = 19. Если результаты совпадут, то последовательность чисел можно будет считать геометрической прогрессией:
