Рассказываем про простой треугольник с необычными свойствами.
В математике есть простая фигура, свойства которой используют во многих областях. С её помощью решают комбинаторные задачи, вычисляют вероятности, строят фракталы и даже разрабатывают криптографические алгоритмы. В этой статье рассказываем про треугольник Паскаля — незамысловатую таблицу чисел с большим потенциалом.
Что такое треугольник Паскаля
Треугольник Паскаля — бесконечный, а его первые десять строк выглядят так:
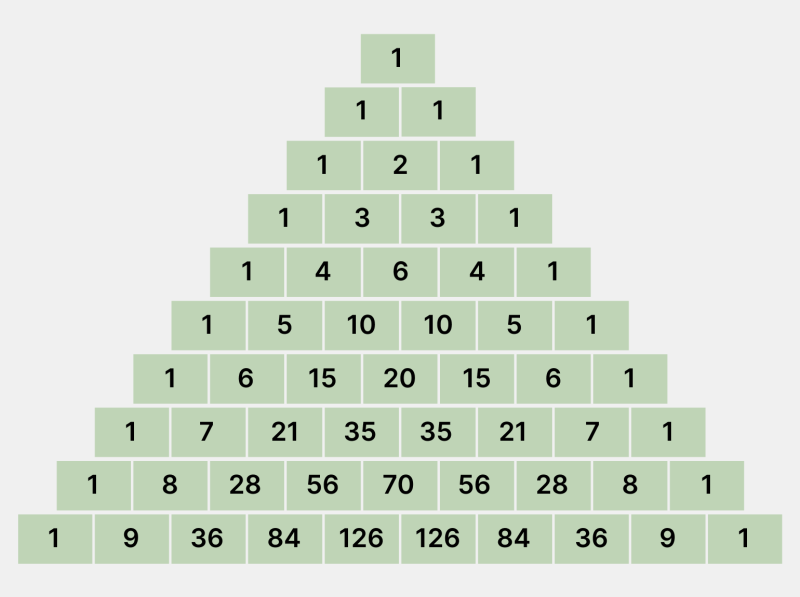
Первые десять строк треугольника Паскаля
Инфографика: Skillbox Media
Треугольник строится по следующим правилам:
- В самом верху стоит единица — это нулевая строка. Нумерация строк (сверху вниз) и элементов (слева направо) начинается с нуля, а не с единицы, как мы привыкли считать.
- На рёбрах треугольника также стоят единицы.
- Каждое число, кроме единиц по бокам, равно сумме двух чисел, стоящих над ним. Например, число 3 в третьей строке равно сумме 1 и 2 из второй строки.
Всё выглядит легко, но, если внимательно изучить треугольник, можно заметить интересные свойства. Давайте рассмотрим их.
Основная формула треугольника Паскаля
Говоря формально, треугольник Паскаля — это расположение биномиальных коэффициентов для положительных целых чисел n и k. Поэтому число каждой ячейки можно найти с помощью рекуррентной формулы:
В ней:
- — элемент в строке n и столбце k;
- — элемент сверху слева;
- — элемент сверху справа.
Если говорить простыми словами, то получится правило, которое мы обозначили выше: каждый элемент равен сумме чисел, стоящих над ним.
Для примера рассмотрим вторую строку треугольника (напоминаем, что нумерация строк начинается с нуля):
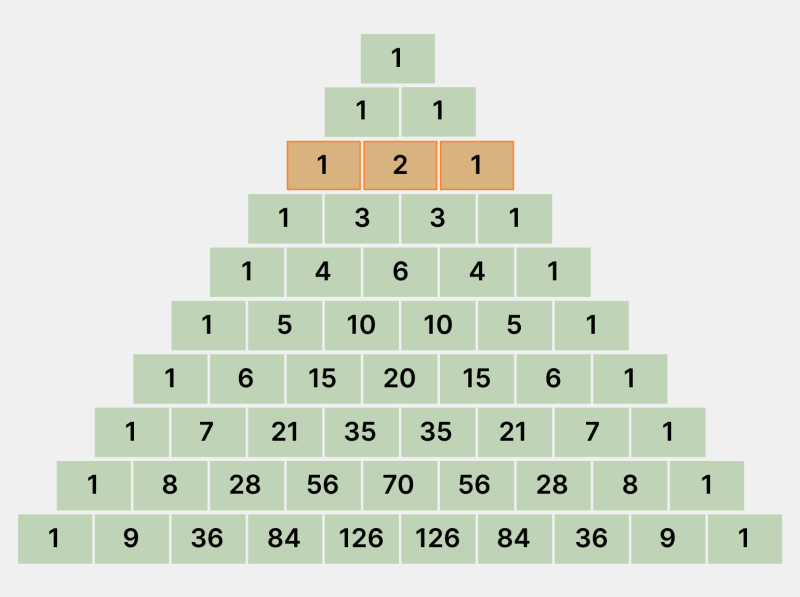
Инфографика: Skillbox Media
Применим рекуррентную формулу, о которой говорили выше, чтобы найти число 2:
Формулу нахождения биномиальных коэффициентов можно записать в аналитическом виде:
Это уже не что иное, как формула сочетаний без повторяющихся элементов из комбинаторики. Она показывает, что элемент k-го столбца n-й строки треугольника Паскаля равен количеству способов выбрать k объектов из n без учёта повторений. Больше узнать про комбинаторику и формулы, которые в ней используют, можно в нашей статье.
Свойства треугольника Паскаля
Треугольник Паскаля так прост, что выписать его сможет даже десятилетний ребёнок. В то же время он таит в себе неисчерпаемые сокровища и связывает воедино различные аспекты математики, не имеющие на первый взгляд между собой ничего общего. Столь необычные свойства позволяют считать треугольник Паскаля одной из наиболее изящных схем во всей математике.
У треугольника Паскаля есть несколько интересных математических свойств. Вот некоторые из них:
- Если провести прямую вертикальную линию по центру треугольника, то части по левую и правую сторону будут симметричны. Например, в строке 1, 4, 6, 4, 1 числа расположены зеркально относительно прямой.
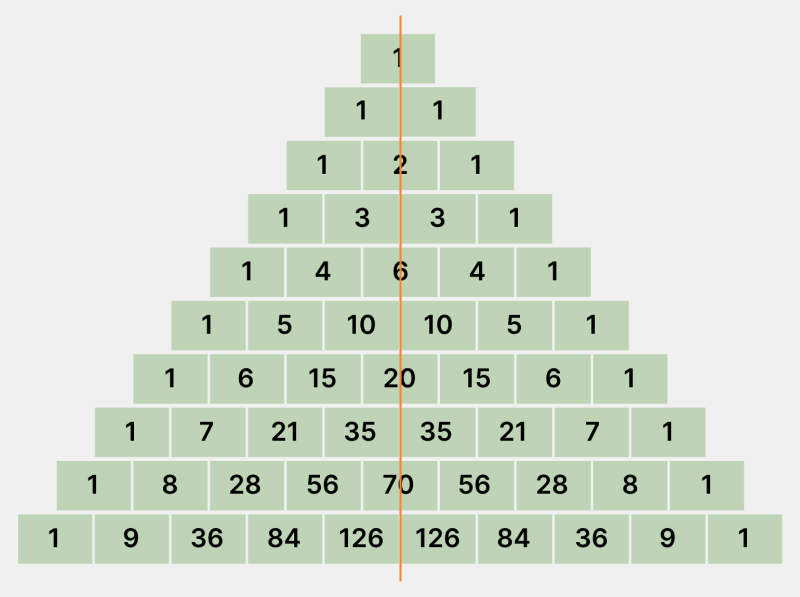
Инфографика: Skillbox Media
- Сумма всех чисел в n-й строке равна 2n. Убедимся в этом и сложим все числа пятой строки: 1 + 5 + 10 + 10 + 5 + 1 = 32 = 25.
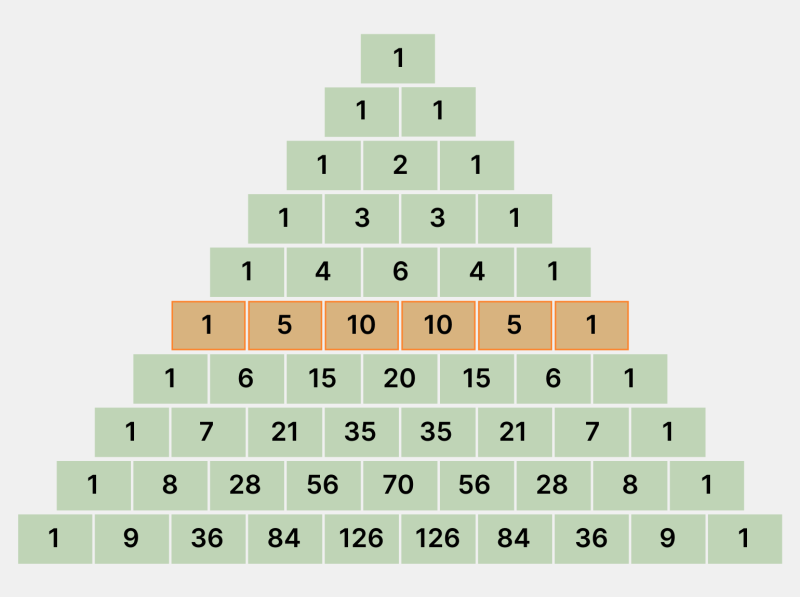
Инфографика: Skillbox Media
- Помимо степени двойки, в треугольнике Паскаля можно найти и квадратные числа. Для этого надо выбрать ячейку и умножить друг на друга все числа, которые её окружают. Например, 1 × 5 × 15 × 21 × 7 × 1 = 11025 = 1052.
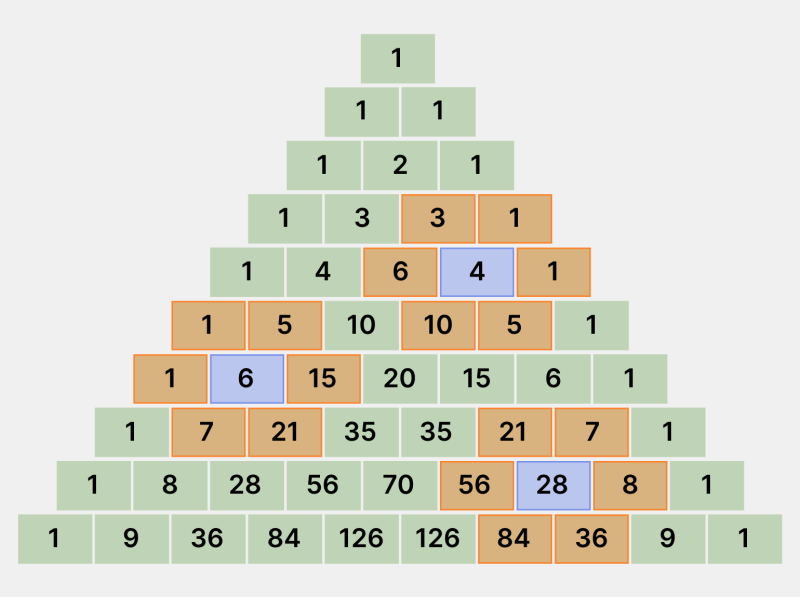
Инфографика: Skillbox Media
- По диагоналям треугольника Паскаля находятся последовательности чисел. На второй диагонали расположены натуральные числа, на третьей находятся треугольные, а на четвёртой — тетраэдральные. На изображении ниже мы построили диагонали справа налево, однако если поменять направление, то последовательности чисел не исчезнут.
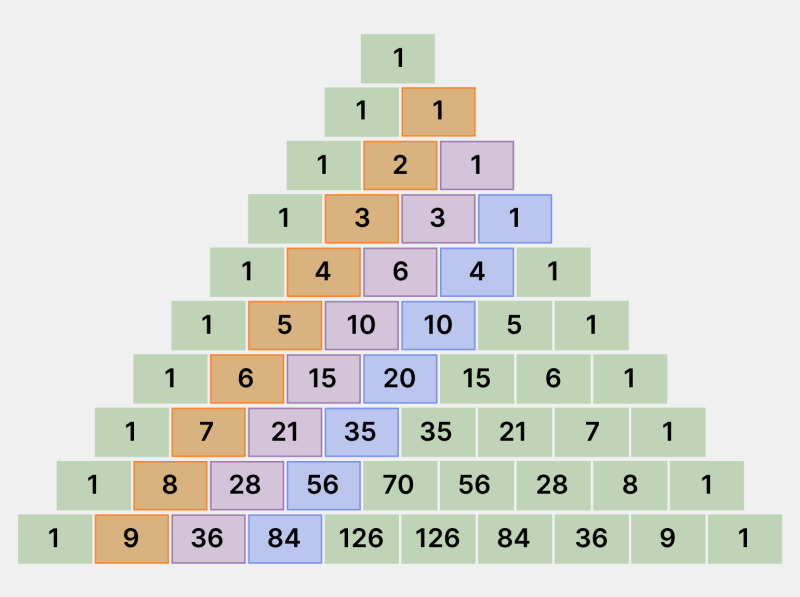
Инфографика: Skillbox Media
- Если второе и предпоследнее число в строке треугольника — простые, то между ними находятся числа, кратные ему. Например, в седьмой строке числа 21 и 35 делятся на простое 7, которое расположено с двух сторон от них их.
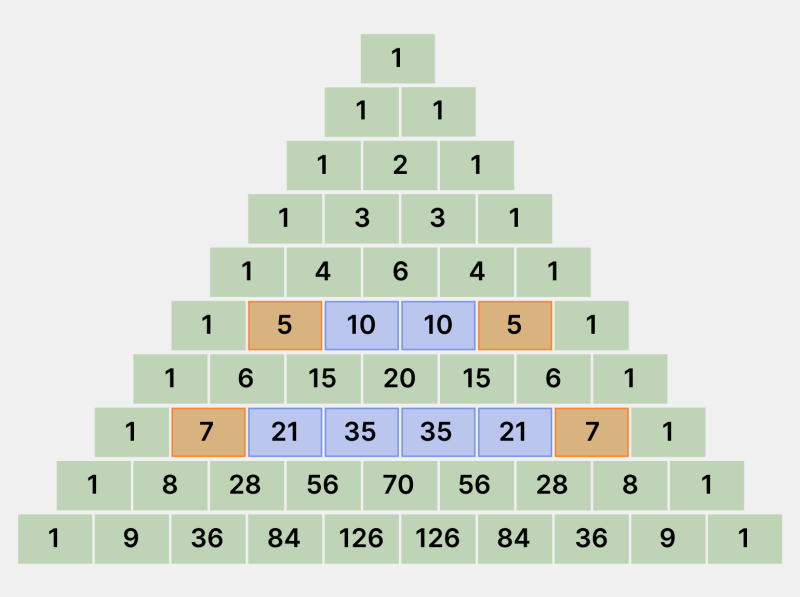
Инфографика: Skillbox Media
- Сумма чисел диагонали равна числу в следующей строке на противоположной диагонали. Проверим это и посчитаем сумму чисел диагонали, которая начинается в пятой строке: 1 + 6 + 21 + 56 = 84.
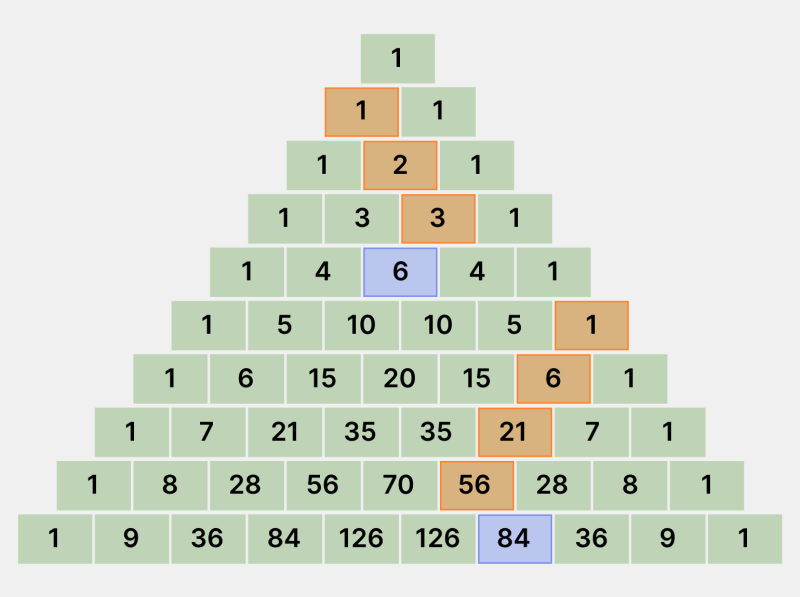
Инфографика: Skillbox Media
- Если из центрального числа строки с чётным порядковым номером вычесть соседнее число той же строки, то мы получим число Каталана.
- Число каждой ячейки треугольника Паскаля равно количеству способов попасть в эту ячейку из вершины.
Где используют треугольник Паскаля
Треугольник Паскаля тесно связан с комбинаторикой. С его помощью можно быстро и без всяких формул узнать количество способов выбрать k объектов из n без учёта повторений. Например, чтобы выяснить, сколькими способами можно взять 3 шара из 5, достаточно посмотреть на третье число в пятой строке.
Помимо комбинаторики, свойства треугольника Паскаля используют в других сферах:
- Алгебра. Выше мы уже говорили о том, что треугольник Паскаля показывает расположение биномиальных коэффициентов. Это значит, что с его помощью можно разложить бином Ньютона.
- Теория вероятностей. Треугольник Паскаля помогает решать задачи на нахождение вероятности того или иного события. Без него для нахождения промежуточных значений пришлось бы использовать формулы.
- Криптография. В некоторых системах шифрования применяют биномиальные коэффициенты, например в криптосистеме Пэйе.
- Фрактальная геометрия. Если построить большой треугольник Паскаля из нескольких десятков строк и закрасить все ячейки с нечётными числами, то получится треугольник Серпинского.

Треугольник Серпинского
Изображение: Samuel Johnson / Wikimedia Commons
Практика: решаем задачи с треугольником Паскаля
Разберём задачи, для решения которых можно использовать треугольник Паскаля.
Задача 1
В кондитерском магазине есть 9 тортов разных видов. Для праздника Ивану надо купить 3 торта. Сколькими способами Иван может выбрать необходимое количество тортов?
Нам надо выбрать 3 объекта из 9 возможных. Значит, смотрим в треугольнике Паскаля на третью ячейку в девятой строке, не забывая, что нумерация строк и ячеек начинается с нуля. В ячейке число 84 — это и есть ответ.
Чтобы убедиться, что треугольник нас не подвёл, посчитаем с помощью формулы сочетаний без повторяющихся элементов:
Задача 2
Разложите выражение (a + b)4.
- Шаг 1. Обратим внимание на степень выражения в скобках: 4. Значит, коэффициентами при разложении будут числа из четвёртой строки треугольника Паскаля: 1, 4, 6, 4, 1.
- Шаг 2. Разложим выражение с помощью формулы бинома Ньютона:
- Шаг 3. Подставим значения биномиальных коэффициентов из треугольника:
Задача 3
Какова вероятность того, что в результате пяти подбрасываний монеты два раза выпадет орёл?
- Шаг 1. Сперва найдём число способов получить 2 орла из 5 бросков. Для этого посмотрим на число во второй ячейке пятой строки треугольника Паскаля: 10.
- Шаг 2. На каждый бросок приходится два варианта исхода событий (орёл или решка), а монету мы подбрасываем пять раз подряд. Значит, общее число исходов равно .
- Шаг 3. Каждый из исходов, когда выпадает орёл — равновозможен. Следовательно, вероятность выпадения двух орлов при пяти подбрасываниях можно найти так:
Что запомнить
- Треугольник Паскаля — математическая таблица, которая показывает расположение биномиальных коэффициентов для положительных целых чисел.
- Каждое число в треугольнике равно сумме двух чисел над ним.
- Числа в строках расположены симметрично относительно центральной оси.
- Сумма чисел в каждой строке равна степени двойки номера строки.
- Свойства треугольника Паскаля используют в комбинаторике, теории вероятностей, алгебре, фрактальной геометрии и криптографии.
Биномиальный коэффициент — число перед членом разложения бинома Ньютона.
Рекуррентная формула — формула, которая выражает следующий член последовательности через предыдущие.
Треугольное число — число точек, которые можно расставить в форме равностороннего треугольника: 1, 3, 6, 10, 15 и так далее.
Тетраэдральные числа — число сфер, из которых можно составить правильный тетраэдр (пирамиду из равносторонних треугольников).
Числа Каталана — последовательность натуральных чисел, которая возникает в комбинаторике и описывает различные структуры, например скобочные последовательности и бинарные деревья.
