Всё, что нужно знать для самостоятельной практики.
Например, скалярное произведение помогает определить угол между персонажем и камерой, что важно для управления её ориентацией и полем обзора. Оно также используется для построения навигации, механики стрельбы и позволяет точно рассчитать освещение объектов в компьютерной графике.
В статье мы рассмотрим свойства скалярного произведения и научимся его вычислять. Начнём с основных терминов и завершим задачами по теме.
Основные определения
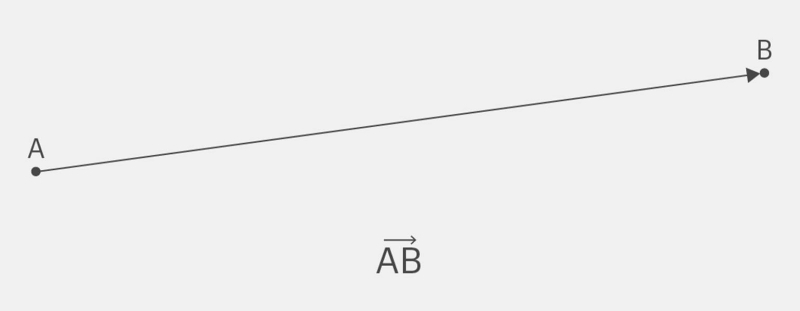
Графическое представление вектора
Инфографика: Skillbox Media
- если угол меньше 90°, векторы направлены в одну сторону;
- если равен 90°, они перпендикулярны;
- если больше 90° — направлены в разные стороны;
- если угол равен 0° или 180° — коллинеарны.
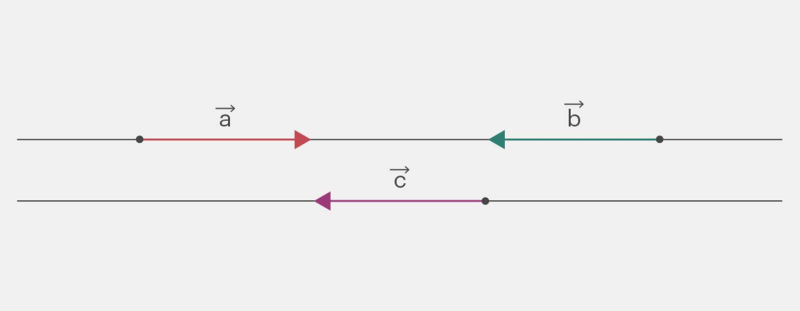
Пример коллинеарных векторов на двух параллельных прямых
Инфографика: Майя Мальгина для Skillbox Media
Как найти скалярное произведение векторов через угол
Воспользуемся следующей формулой:
В этой формуле: и — выбранные векторы; и — их длины (модули), а — угол между ними.
Геометрический смысл скалярного произведения заключается в том, что оно выражает величину проекции одного вектора на другой. Эту проекцию можно представить как «тень» одного вектора на ось направления другого. Чем больше векторы направлены в одну сторону, тем больше их проекция друг на друга. Если они направлены в противоположные стороны, их проекции уменьшаются и могут быть отрицательными — то есть «тень» одного вектора лежит в противоположном направлении относительно оси другого.
Представьте двух человек, тянущих верёвку в одном направлении. Поскольку они работают сообща, их усилия складываются и результат будет положительным — как положительное скалярное произведение векторов.
Теперь перейдём к расчёту. Допустим, длина равна 3, а длина — 4, а угол между ними — 30°. Вычислим скалярное произведение:
Другая ситуация: первый человек тянет верёвку в одну сторону, а другой — в противоположную. Из-за этого их усилия работают друг против друга и результат может стать отрицательным. Оставим наши векторы с длинами 3 и 4, но изменим угол между ними на 120° и посчитаем:
Третья ситуация: оба человека тянут верёвку под прямым углом и их усилия не влияют друг на друга. Возьмём два наших вектора и изменим угол на 90°:
Если вы разработчик и вам нужно вычислять скалярное произведение на основе различных параметров, это удобно делать с помощью математических калькуляторов. Например, на сайте onlinemschool.com можно просто подставить значения и не вникать в смысл формул.
Однако, если вам нужно глубоко разобраться в геометрическом смысле скалярного произведения, проекции векторов и прочих параметрах, рекомендуем бесплатный сервис desmos.com. Это визуальный геометрический калькулятор, который позволяет вводить различные формулы и сразу видеть, что происходит.
Пример положительной проекции одного вектора на другой
Скриншот: Desmos
Как найти скалярное произведение векторов по координатам
Если нам неизвестны длины векторов и угол между ними, для вычисления скалярного произведения мы можем использовать координаты векторов. Речь идёт о прямоугольной системе координат, состоящей из взаимно перпендикулярных осей. В двумерном пространстве для обозначения этой системы обычно используются оси X и Y, а в трёхмерном — оси X, Y и Z.
Можно представить вектор как стрелку, исходящую из начала координат и заканчивающуюся в определённой точке. Эта точка окончания вектора определяет его координаты. Из этой точки мы можем провести перпендикуляры на оси системы координат, чтобы получить прямоугольные треугольники и по ним рассчитать длину наших векторов.
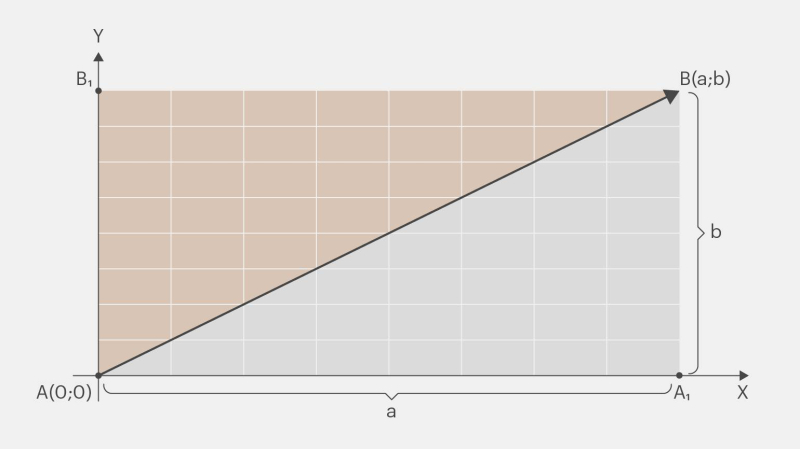
Вектор в системе координат — это гипотенуза прямоугольного треугольника.
Инфографика: Skillbox Media
В двумерном пространстве нам необходимо перемножить соответствующие координаты векторов и сложить полученные произведения:
В этой формуле:
- x1 и y1 — координаты ;
- x2 и y2 — координаты .
Добавим векторам координаты и посчитаем. Возьмём с координатами (3, 4) и с координатами (2, 5):
В трёхмерном пространстве мы также перемножаем соответствующие координаты и затем складываем полученные произведения. Изменим координаторы (1, 2, 3) и (4, 5, 6), а затем вычислим результат:
Свойства скалярного произведения векторов
У скалярного произведения есть несколько свойств, о которых важно знать перед решением задач. Эти свойства позволяют упростить вычисления.
Этот результат часто используется для вычисления длины вектора. Для примера возьмём с координатами (3, 4) и найдём его длину:
Теперь используем скалярное произведение:
Получаем доказательство нашего свойства:
- если = 0 или = 0, то ;
- если векторы перпендикулярны (), то .
Задачи для самопроверки на нахождение скалярного произведения векторов
Задача №1
Найдите скалярное произведение двух векторов длиной 5 и 7 единиц с углом 60° между ними.
Вычисляем скалярное произведение через угол по формуле:
Задача №2
Найдите скалярное произведение векторов с такими значениями:
= (2, 3, −1) и = (−1, 4, 0).
Вычислим значение по формуле через координаты:
Подставляем значения и считаем:
Задача №3
Проверьте, являются ли = (1, 2, −3) и = (3, −6, 1) ортогональными (перпендикулярными).
Векторы перпендикулярны, если их скалярное произведение равно нулю. Найдём произведение через координаты и проверим результат:
В нашем случае скалярное произведение не равно нулю, и это значит, что векторы не перпендикулярны.
Задача №4
У нас есть два вектора: = (4, 3) и = (6,0). Известно, что их скалярное произведение равно 24. Найдите угол между ними.
Скалярное произведение выражается через угол по формуле:
Из формулы мы можем выразить угол:
Теперь нам нужно рассчитать длины векторов:
Подставляем значения в формулу и находим косинус угла:
Мы нашли косинус угла, осталось найти сам угол. Для этого переходим на сайт onlinemschool.com и подставляем значение в «Калькулятор — арккосинус угла». Арккосинус — это обратная функция к косинусу. В нашем случае угол между векторами будет приблизительно равен 36,87°.
