Её можно интегрировать в более крупные языковые модели.
Исследовательская группа Microsoft Research Asia, специализирующаяся на математике и искусственном интеллекте, разработала малую языковую модель (SLM) под названием rStar-Math для решения математических задач. В своей статье, опубликованной на сервере препринтов arXiv, команда подробно описала технологические аспекты, математические принципы и результаты тестирования нового инструмента.
Подробнее про SLM
Малые языковые модели (SLM) характеризуются низкой ресурсозатратностью и способны работать локально на устройстве. Такие модели оптимально применять для узкоспециализированных задач и ответов на вопросы в определённых областях. Microsoft сфокусировала внимание на обучении SLM не только в области, касающейся математических навыков, — разработчики сконцентрировались на развитии навыка формировать логические рассуждения при анализе проблемы.
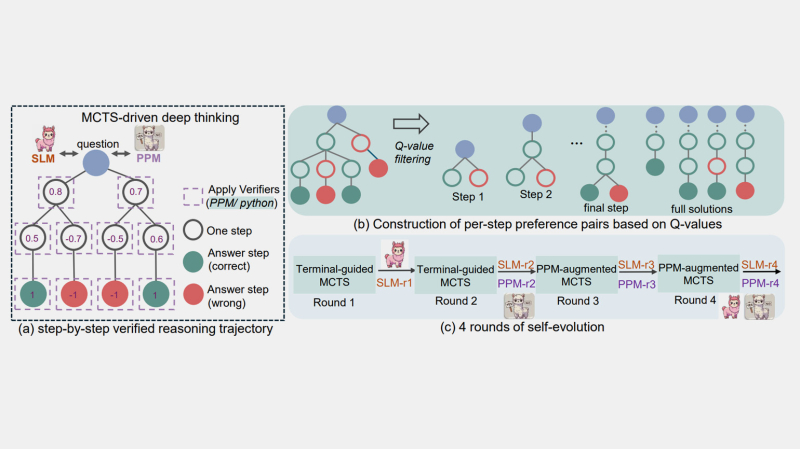
Изображение: rStar-Math: Small LLMs Can Master Math Reasoning with Self-Evolved Deep Thinking / Xinyu Guan / Li Lyna Zhang / Yifei Liu / Ning Shang / Youran Sun / Yi Zhu / Fan Yang / Mao Yang
Одной из целей разработки rStar-Math стала интеграция SLM в более крупные языковые модели (LLM), которая может открыть перспективы для их совместного использования. Примечательно, что выпуск rStar-Math последовал вскоре за презентацией другой компактной модели Microsoft — Phi-4, также ориентированной на математические задачи.
Ключевые особенности
rStar-Math отличается от Phi-4 использованием метода Монте-Карло. Этот подход имитирует человеческое пошаговое мышление, позволяя разбивать сложные задачи на более простые элементы. Выводы модели представлены как в виде Python-кода, так и на естественном языке.
В rStar-Math реализованы три ключевых новшества:
1. Метод синтеза данных с дополнением кода — с помощью метода Монте-Карло создаются пошаговые рассуждения.
2. Метод обучения с вознаграждением за процесс — он исключает необходимость аннотирования промежуточных шагов.
3. Рецепт саморазвития — модель и её предпочтения развиваются по итеративному принципу с нуля.
Результаты тестов
После четырёх раундов обучения на миллионах синтезированных решений для 747 тысяч задач rStar-Math продемонстрировала значительные результаты. На тесте MATH точность моделей Qwen2.5-Math-7B и Phi3-mini-3.8B возросла с 58,8% до 90,0% и с 41,4% до 86,4% соответственно, превзойдя показатели o1-preview на 4,5% и 0,9%. На математической олимпиаде США (AIME) rStar-Math решила в среднем 53,3% задач (8 из 15).
Команда планирует опубликовать исходный код и данные rStar-Math на GitHub, сделав их общедоступными.