Знакомимся с разбросом данных и учимся его рассчитывать.
Чемпион по дартсу и математик зашли в паб, выпили по кружке пенного и начали бросать дротики. Математик заметил, что у бросков чемпиона низкая дисперсия. Давайте разберёмся и выясним:
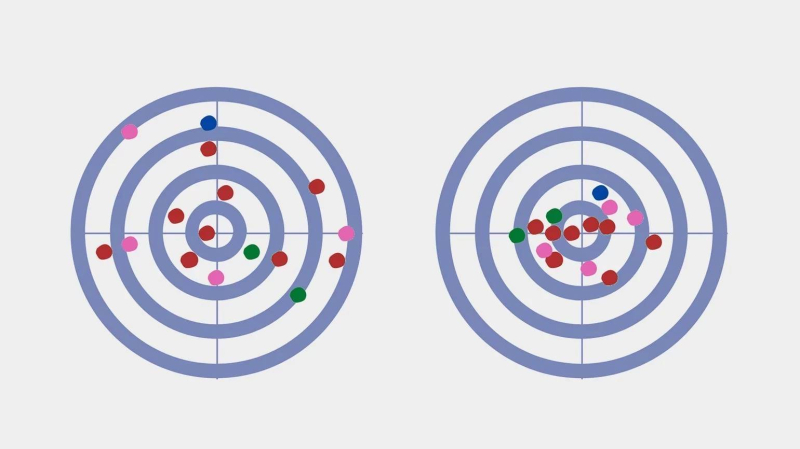
Слева — мишень математика, справа — мишень чемпиона по дартсу с низкой дисперсией
Изображение: Skillbox Media
Понятие и виды дисперсии
Дисперсия в статистике — это показатель разброса данных вокруг их среднего значения. Высокая дисперсия указывает на большой разброс данных, а низкая — на их близость друг к другу. Рассмотрим примеры:
- 1, 2, 3, 4, 5 — числа находятся в пределах ±2 от среднего значения 3, поэтому дисперсия низкая;
- 13, 25, 976, 90, 120 713 — здесь дисперсия высокая, так как разница между наименьшим и наибольшим числом превышает 120 000.
Дисперсия случайной величины позволяет оценить уровень отклонения данных от их среднего значения. Допустим, средний балл на экзамене 75 из 100. Зная дисперсию, можно определить вероятность того, что конкретный студент получит результат, значительно отличающийся от 75 баллов:
- при высокой дисперсии баллы студентов будут сильно различаться, что увеличивает вероятность отклонений;
- при низкой дисперсии баллы близки к среднему значению, поэтому вероятность значительных отклонений небольшая.
Генеральная рассчитывается для всей совокупности данных, когда известны значения всех элементов. То есть мы можем определить генеральную дисперсию для результатов ЕГЭ по математике в регионе, если известны баллы всех выпускников.
Примеры использования
Дисперсия применяется в экономике, социологии, инвестициях и других областях, где важно анализировать и оценивать данные.
С дисперсией обычно работают учёные, статистики, аналитики, ML-инженеры и другие специалисты:
- Учёные используют её для анализа результатов экспериментов. Например, в медицинских исследованиях она помогает оценить, насколько различаются реакции пациентов на лечение и насколько эффективно оно работает в целом.
- Статистикам дисперсия нужна для анализа данных и построения надёжных моделей. Она помогает оценить точность модели прогнозирования спроса на товары, определяя, насколько предсказанные значения соответствуют фактическим.
- Аналитикам она помогает оценивать стабильность и эффективность бизнес-процессов. Например, можно проанализировать продажи по регионам, чтобы выявить успешные и проблемные зоны для расширения бизнеса.
- ML-инженеры используют дисперсию в машинном обучении для оценки разброса предсказаний моделей. Например, в модели классификации высокий разброс указывает на возможные ошибки в обучении модели и неправильное отображение данных.
Формулы и порядок расчёта дисперсии
Если известны все элементы совокупности данных, мы можем вычислить генеральную дисперсию (случайную величину):
Элементы формулы расчёта дисперсии случайной величины:
- σ2 — генеральная дисперсия;
- N — количество элементов в совокупности;
- xi — значение элементов;
- μ — среднее значение элементов.
Возьмём небольшой набор данных и поэтапно вычислим для него генеральную дисперсию: 2, 4, 4, 4, 5, 5, 7, 9.
Результаты вычислений:
- (2 − 5)2 = (−3)2 = 9;
- (4 − 5)2 = (−1)2 = 1;
- (4 − 5)2 = (−1)2 = 1;
- (4 − 5)2 = (−1)2 = 1;
- (5 − 5)2 = (0)2 = 0;
- (5 − 5)2 = (0)2 = 0;
- (7 − 5)2 = (2)2 = 4;
- (9 − 5)2 = (4)2 = 16.
Мы получили значение генеральной дисперсии, равное 4.
Если у нас есть только часть совокупности данных, мы можем использовать формулу выборочной дисперсии:
Элементы формулы расчёта дисперсии ряда чисел:
- s2 — выборочная дисперсия;
- n — количество элементов в выборке;
- xi — значение каждого элемента;
- x̅ — среднее значение выборки.
Порядок расчёта выборочной дисперсии почти не отличается от генеральной. Разница лишь в том, что в формуле выборочной дисперсии используется корректировка на размер выборки n − 1, а в генеральной дисперсии — общее количество элементов N.
Связь дисперсии с другими статистическими показателями
Среднее арифметическое, стандартное отклонение и коэффициент вариации — это показатели, которые вместе с дисперсией помогают оценить разброс данных относительно их центрального значения.
В отличие от стандартного отклонения, дисперсия измеряется в квадратных единицах и поэтому чаще используется в теоретических и математических расчётах, где нужны точные статистические оценки.
Дисперсия также связана с другими статистическими показателями, например асимметрией и эксцессом. Они помогают лучше понять форму распределения данных, но их сложнее интерпретировать.
Волатильность — это степень изменчивости цены или доходности актива за определённый период. Чем выше волатильность, тем сильнее колебания. Например, акции стартапов могут иметь высокую волатильность из-за нестабильности их бизнеса. А вот государственные облигации обычно имеют низкую волатильность, поскольку их доходность стабильна и предсказуема.
Стратегия распределения инвестиций между различными видами активов. Если инвестор вложит деньги в акции одной компании, доходность его портфеля будет зависеть от изменения их стоимости. Но если он распределит свои инвестиции между акциями нескольких компаний, облигациями и недвижимостью, то, даже если один из инструментов покажет плохие результаты, другие активы могут компенсировать потери.
Модели классификации в машинном обучении — это алгоритмы, которые назначают объекты или данные к одной из заранее определённых категорий на основе их характеристик. Например, по содержимому электронного письма модель классификации может определять, является ли оно спамом.
