Сети Колмогорова-Арнольда появились совсем недавно, но уже успели произвести фурор благодаря совершенно новой архитектуре. Рассказываем, что это такое и как они помогают в обучении Graph.
В середине XX века математики Андрей Колмогоров и Владимир Арнольд вывели авторскую теорему, которая гласит, что любую непрерывную функцию нескольких переменных можно представить как суперпозицию функций одной переменной и операций сложения (а если говорить коротко, то одну сложную задачу всегда можно разложить на несколько простых).
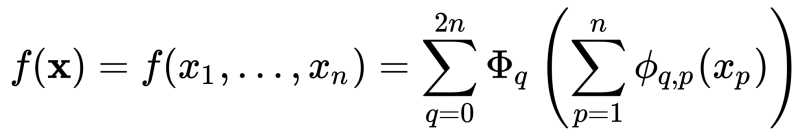
Теорема Колмогорова-Арнольда
Теорема Колмогорова-Арнольда используется в процессе создания нейросетей, которые легко обучаются для выполнения трудных задач. Она предлагает гибкий способ моделирования сложных функций.
Что такое сети Колмогорова-Арнольда
Теорема Колмогорова-Арнольда легла в основу KAN — современных нейронных сетей, которые обещают превзойти все уже существующие программы. Разработали их, кстати, совсем недавно — в MIT.
Вот несколько их свойств:
- Фрактальная структура. KAN обладают фрактальными свойствами (выглядят одинаково на всех масштабах).
- Иерархическая вложенность. Сети Колмогорова-Арнольда имеют иерархическую структуру, на которой каждый уровень вложенности описывается похожим характером.
- Самоподобие. Структура KAN повторяется на разных масштабах.
- Хаотическое поведение. Сети Колмогорова-Арнольда могут демонстрировать хаотическое поведение. Это означает, что даже небольшие изменения в начальных условиях могут привести к значительным различиям в исходных данных.
- Каскадное разрушение. При некоторых параметрах сети Колмогорова-Арнольда способны проявлять каскадное разрушение. Итогом этого процесса становится динамика, в ходе которой состояние системы периодически меняется между хаосом и порядком.
- Простота описания. Сети Колмогорова-Арнольда представляют собой простую модель, которая может с легкостью анализировать и понимать поведение хаотических систем.
У сетей Колмогорова-Арнольда есть большой спектр практических применений. В него входит математическое моделирование сложных систем, сетевая теория, биология, физика и другие науки. А в течение последних лет KAN помогли в изучении интернет-трафика и социальных сетей.
Архитектура KAN
Из чего состоит архитектура перцептрона — самой простой формы нейросетей?
Альтернатива JetBrains: обзор GIGA IDE от Сбераtproger.ru
Основа работы всех нейросетей — функции. В любой задаче у программы есть обучающая выборка, которая включает в себя пары {xi, yi} (x — входные данные, y — ответ). А сама сеть должна найти функцию, которая обобщает входы и выходы задачи.
Архитектура перцептрона ищет такую функцию, используя линейные слои. На них происходит умножение входов на вес ребер и функций активации в нейронах (этот процесс работает на основе теоремы Цыбенко, которая утверждает, что нейросеть может заменить непрерывную функцию более простой с любой точностью).
В отличие от перцептрона у сетей Колмогорова-Арнольда нет ни линейных весов, ни функций активации в нейронах. На ребрах сетей в KAN происходит работа над обучением функций, а в нейронах их значения складываются.
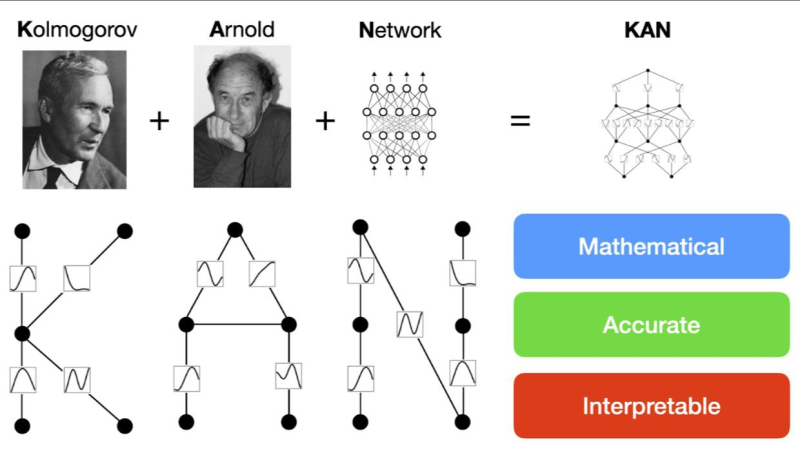
Основа работы сетей Колмогорова-Арнольда
Также в сетях Колмогорова-Арнольда есть непрерывные сплайны, благодаря которым в обучении KAN не возникает сложностей. Гладкая кривая, называемая сплайном, представляет собой кусочно-полиномиальную функцию, которая задается полиномами на разных отрезках. Для аппроксимации каждого сплайна использу.тся определенные точки. Точность аппроксимации зависит от их количества: чем больше точек, тем лучше результат.
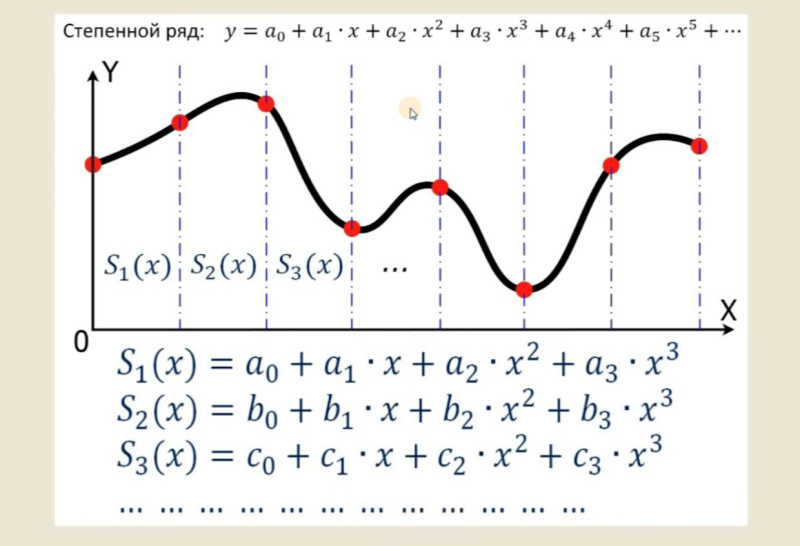
Сплайны в сетях Колмогорова-Арнольда
Чем KAN отличается от MLP
- В сетях Колмогорова-Арнольда функции активации находятся на ребрах, в то время как в MLP (нейронной сети с прямой связью) они размещены в узлах.
- У KAN и MLP одинаковая точность выполнения задач. А иногда сети Колмогорова-Арнольда даже превышают точность MLP при маленьком количестве вычислений и нейронов.
- KAN легко визуализировать. Вы можете запросто посмотреть, что умеет каждая функция сетей.
- Но у сетей Колмогорова-Арнольда есть и недостаток. В отличие от MLP они медленно обучаются, но создатели KAN планируют это изменить в скором времени.
Минусы в работе сетей Колмогорова-Арнольда
Да, даже у такой мощной модели при всех огромных плюсах есть и недостатки:
- Высокая сложность в обучении. KAN достаточно трудно строить и обучать. Но если вы хотите полноценно работать с нейросетями, вам придется с этим смириться — с ними просто невозможно подружиться без больших количеств данных и вычислений.
- Неустойчивость к шуму. Сети Колмогорова-Арнольда резко и чувствительно реагируют на неправильно подсчитанные и введенные данные.
- Ограниченные области применения. KAN, в отличие от других нейронных сетей, более ограничены в использовании в различных задачах машинного обучения.
- Требования к объему данных. Сети Колмогорова-Арнольда нуждаются в большом объеме обучающих данных для достижения хороших результатов. Однако при ограниченном доступе данных достать их непросто.
- Необходимость тщательной настройки гиперпараметров. Для достижения оптимальной производительности KAN требуется тщательная настройка гиперпараметров, что может потребовать дополнительного времени и усилий.
Graph Learning, или обучение графов
Графы — один из лучших способов представления данных. С их помощью можно представить все виды данных: начиная от создания лекарств и заканчивая разработкой роботов.
А ещё графы — это структуры данных в виде сетей с внутренними парнями связями. Обычно они изображены в виде «узлов» и линий (или же рёбер). Правда, в традиционном подходе к обучению графов хватает проблем. Вот некоторые из них:
- Недостаток данных. Чтобы обучать графы, нужно огромное количество размеченных данных, которые не так уж и просто получить для сложных и больших графов.
- Вычислительная сложность. Обработка графов может быть трудной задачей из-за их большого размера и сложной структуры.
- Недостаток интерпретируемости. Некоторые графовые модели могут быть сложными для интерпретации, что затрудняет понимание принимаемых ими решений.
- Недостаточная устойчивость к шуму. Графовые модели могут быть чувствительны к шуму и выбросам данных, а это может привести к неправильным прогнозам или классификациям.
Как KAN улучшают обучение Graph
Применение сетей Колмогорова-Арнольда в обучении Graph может улучшить работу путем:
- Анализа структуры графа. KAN изучают структуру и связи в графах. Это способствует пониманию его отличительных черт и определению проблем в его системе.
- Прогнозирования поведения графа. Сети Колмогорова-Арнольда умеют предсказывать изменения в графе и его дальнейшей работе, что позволяет с легкостью принимать решения на основе данных KAN.
- Оптимизации работы с данными. Сети Колмогорова-Арнольда оптимизируют работу со структурой графа, упрощают процесс взаимодействия с данными и улучшают производительность.
- Идентификации ключевых элементов. KAN способны «вывести наружу» главные узлы или связи в графе, благодаря чему можно уделить большее внимание важным аспектам работы и сделать деятельность эффективнее.
Например, в классическом Graph Learning может возникнуть проблема передачи информации между далёкими узлами в графе, что требует сложных механизмов агрегации информации. Внедрение KAN позволит аппроксимировать такие зависимости через более простые функции, что улучшит скорость обучения и качество финального предсказания.
Получается, что применение KAN в Graph позволит лучше разобраться в структуре данных, оптимизировать работу с графами, а также предсказывать и контролировать их поведение.
Реализация и применение KAN в разных областях
Реализация сетей Колмогорова-Арнольда нуждается в большом объеме знаний в области нейросетей, динамических систем и математического моделирования. Как правило, для обучения KAN применяют библиотеки TensorFlow или PyTorch.
Для того чтобы понять процесс реализации сетей Колмогорова-Арнольда, необходимо с головой окунуться в статьи и учебные пособия на тему нейросетей. Также стоит использовать практические знания по программированию на Python и математике для создания и обучения моделей КАN.
Как мы уже говорили, сети Колмогорова-Арнольда активно применяются во многих областях. Вот некоторые из них:
- Обработка изображений. KAN используются в сегментации изображений и их классификации. Они обучаются глубоким представлениям изображений и избегают проблем затухания градиентов.
- Обработка естественного языка. Сети Колмогорова-Арнольда применяются в машинном переводе, анализе и генерации текста. Они извлекают высокоуровневые признаки из текстовых данных, что помогает улучшить качество предложений.
- Рекомендательные системы. KAN используются в системах для прогнозирования пользовательских предпочтений и рекомендации контента. Кроме того, KAN ускоряют контент и облегчают доступ к информации.
- Медицинский анализ данных. Сети Колмогорова-Арнольда применяются в медицинской диагностике, сегментации медицинских изображений, анализе медицинских данных и прочих областях медицины. KAN могут извлекать сложные характеристики и улучшать точность и скорость диагностики.
- Наука. Сети Колмогорова-Арнольда активно применяются в развитии моделирования и анализа различных научных явлений (генетика, экология, физика, социология и другие). С помощью KAN ученые с легкостью могут исследовать сложные взаимосвязи между элементами системы, выявлять закономерности и прогнозировать поведение системы.
Несколько примеров, как применяются KAN:
- Теория хаоса. Сети Колмогорова-Арнольда помогают в изучении хаотического поведения систем в физической, экологической, экономической и биологической областях.
- Криптография. KAN активно используются в процессе создания криптографических алгоритмов и методов шифрования, в основу которых ложится хаос.
- Компьютерная наука. Системы Колмогорова-Арнольда могут служить «палочкой-выручалочкой» во время работы над алгоритмами машинного обучения и искусственного интеллекта.
- Физика. KAN работают в моделировании физических систем (плазма, динамика жидкостей, кристаллические структуры).
Сети Колмогорова-Арнольда действительно выглядят многообещающе, учитывая, что их архитектура радикально отличается от привычных MLP. Разумеется, без недостатков тоже не обошлось, однако со временем KAN может стать наиболее совершенной моделью, которая справляется с задачами любой сложности и динамики.
