Числа, которыми можно измерить всё.
Почти всё вокруг нас можно посчитать, измерить, закодировать и представить в виде чисел. В математике есть множество чисел, которыми можно описать практически все окружающие нас предметы и явления. Они называются действительными, или же вещественными.
В этой статье рассказываем, что такое действительные числа, откуда они взялись, где применяются, чем они отличаются от других и как представлены в памяти компьютера.
Определение действительных чисел
- Натуральные числа (N) — это числа, которые мы используем во время порядкового счёта: 1, 2, 3, 4, 5, …
- Целые числа (Z) — все натуральные числа, отрицательные числа и ноль: … −3, −2, −1, 0, 1, 2, 3, 4, 5, …
- Рациональные числа (Q) — это дроби, которые можно записать как отношения двух целых чисел: ½, 0,5, −0,3333, …
- Иррациональные числа (I) — это числа с бесконечным не повторяющимся значением после запятой — например, число π, √2.
Множество действительных чисел обозначается латинской буквой R. Посмотрите на схему ниже и обратите внимание, как одно множество связано с другими:
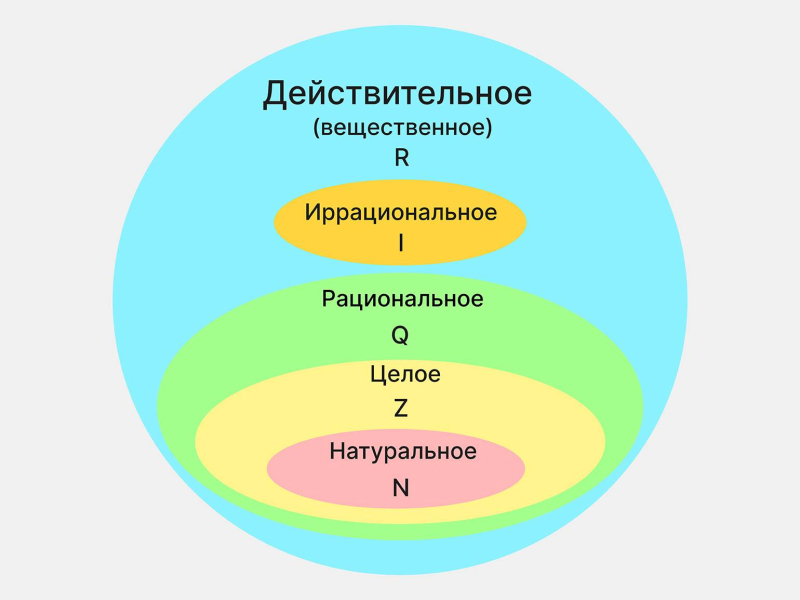
Схема множеств чисел, которые входят во множество действительных чисел
Инфографика: Skillbox Media
Эту схему можно записать в виде математического выражения N ∈ Z ∈ Q ∈ R, где ∈ означает «относится». То есть натуральное множество относится к целому, целое — к рациональному, а рациональное — к действительному.
По сути, действительные числа — это все числа, которые мы используем в повседневных и научных расчётах. Их как раз и придумали для того, чтобы измерять физические и геометрические величины — а ещё они нужны для извлечения корня, вычисления логарифмов, исследования функций и решения алгебраических уравнений.
Координатная прямая и действительные числа
Наглядно представить действительные числа можно с помощью координатной прямой.
У координатной прямой есть несколько важных особенностей:
- Точка отсчёта. По центру координатной прямой есть точка, которая обозначается как ноль (0). Это отправная точка, относительно которой отмечают другие числа. Слева находятся числа, которые меньше нуля, справа — больше.
- Направление. Числа на координатной прямой увеличиваются слева направо.
- Равные расстояния. Все числа на координатной прямой располагаются с равными промежутками друг между другом. Например, между 0 и 1 расстояние будет такое же, как между −1 и 0.
- Дроби и иррациональные числа. На координатной прямой можно отобразить не только целые числа, но и дробные (0,75, ½), а также иррациональные (√2, π).
На координатной прямой можно отобразить только действительные числа. Комплексные числа на прямой разместить не получится, потому что у них есть дополнительная, «мнимая» часть, которая требует отдельной оси.
Для примера отобразим некоторые действительные числа на координатной прямой:
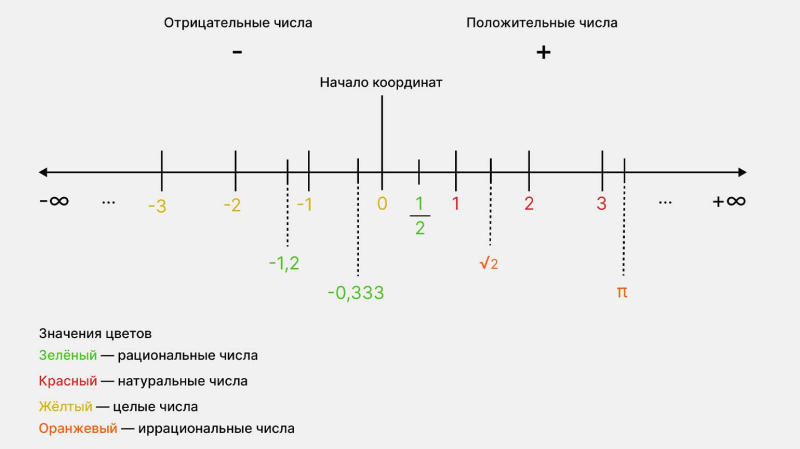
Действительные числа на координатной прямой
Инфографика: Skillbox Media
Представление действительных чисел
Есть несколько способов представления действительных чисел. Чаще всего встречается десятичное представление — когда число записывают в десятичной форме с использованием целой и дробной части.
Десятичное представление бывает конечным или бесконечным. В первом случае после запятой есть фиксированное количество чисел, а во втором — числа после запятой никогда не заканчиваются.
Например, число 3,14159265… — десятичное представление числа π (Пи).

Десятичное представление числа
Инфографика: Skillbox Media
Рациональные числа действительного множества можно записать в виде дроби. В общем виде дробь записывается как отношение двух целых чисел m и n: . Число m называется числителем, а n — знаменателем.
Например, рациональное число 0,5 можно перевести в дробный вид. Получится дробь . А вот иррациональное число 3,14159265… записать в виде дроби не выйдет.

Дробное представление числа
Инфографика: Skillbox Media
Большие действительные числа можно записать в экспоненциальном виде — это представление числа в виде мантиссы и порядка. Такой способ позволяет сократить запись числа, например, если в нём много нулей.
Рассмотрим, как формируется экспоненциальная запись на примере числа 1 000 000 (один миллион):
- Старший разряд в 1 000 000 — единица (1). Это и есть мантисса числа.
- Теперь разложим 1 000 000 как степень десяти. Получится 1 000 000 = 10 × 10 × 10 × 10 × 10 × 10 = 106. Степень указывает на количество нулей после мантиссы.
- Объединим два этих числа в экспоненциальной записи и получим 1 000 000 = 1 × 106.
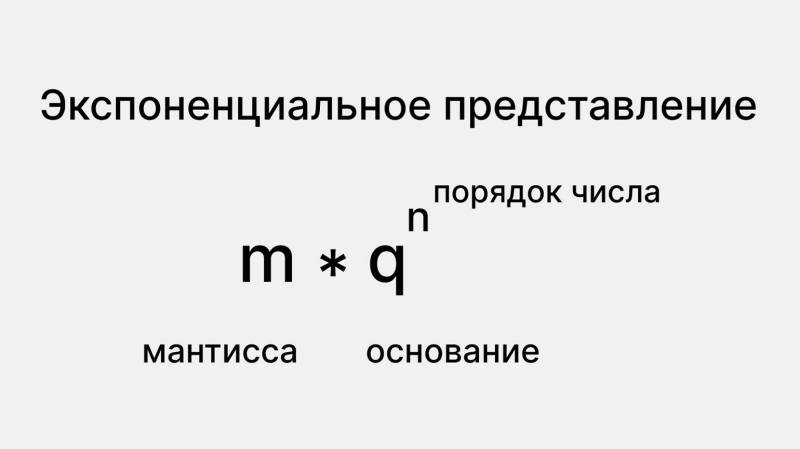
Экспоненциальное представление числа
Инфографика: Skillbox Media
Вещественные числа в памяти компьютера
Все числа в памяти компьютера хранятся в двоичном виде, то есть состоят из нулей и единиц. В языках программирования для хранения вещественных чисел предусмотрены типы данных float и double. Они представляют числа с помощью экспоненциальной записи. Если перевести число в битовый вид, получится запись, состоящая из трёх частей: положительного или отрицательного знака, порядка (экспоненты) и мантиссы.
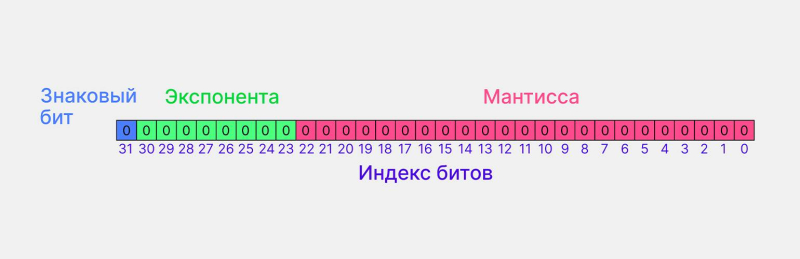
Экспоненциальное представление битов в памяти компьютера
Инфографика: Skillbox Media
Чтобы быстрее это понять, разберём, как хранится в памяти компьютера округлённая до сотых запись числа Пи (3,14).
Для начала заполним знаковый бит. Если число положительное, то он будет равен нулю, если отрицательное — единице. 3,14 — положительное число, значит, в 31-й индекс вписываем 0:
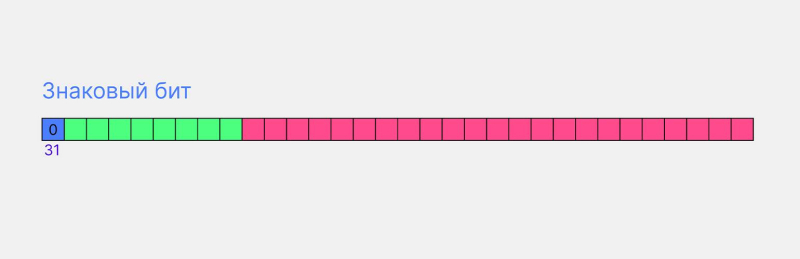
Знаковый бит числа Пи
Инфографика: Skillbox Media
Теперь вычислим двоичную мантиссу. Для этого сначала переведём целую часть в двоичное представление: 310 = 112. То же самое сделаем с дробной частью: 0,1410 = 0,00100011110101110000112.
Если подзабыли, как переводить числа из десятичной системы в двоичную, почитайте наш материал о десятичной системе счисления. А ещё можно воспользоваться калькулятором для программистов.
Получившееся значение переведём в экспоненциальный вид — так, чтобы в целой части была одна единица. После преобразований число 11,00100011110101110000112 превратится в 1,100100011110101110000112 × 21.
1,10010001111010111000011 — это мантисса, а основание равно двум, потому что мы имеем дело с двоичной системой счисления. Откидываем целую часть, а всё остальное вписываем в индексы с 22-го по 0-й:
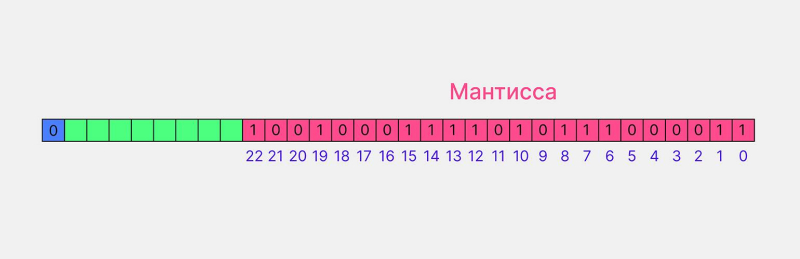
Двоичная мантисса
Инфографика: Skillbox Media
Осталось найти двоичную экспоненту — то, на что умножается наша мантисса. Для этого складываем степень основания 1 с числом 127: 1 + 127 = 128. 127 — это константное значение смещения экспоненты. Оно прибавляется, чтобы не тратить бит на знак степени у экспоненты.
Теперь переводим получившееся значение в двоичный вид и вписываем его в оставшиеся индексы — с 30-го по 23-й: 12810 = 100000002.
В итоге получим 0 10000000 10010001111010111000011. Именно так число 3,14 хранится в памяти компьютера.
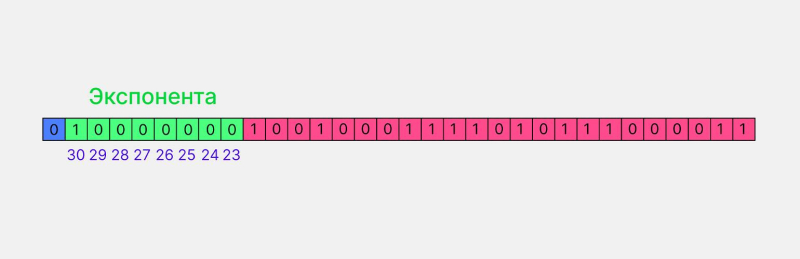
Двоичная экспонента
Инфографика: Skillbox Media
Странности при работе с вещественными числами
Предыдущий пример — обобщённый. Он нужен для понимания того, как компьютер работает с вещественными числами. В реальности при работе компьютера с действительными числами часто возникают погрешности.
Например, если в языке Java сложить числа 0,2 и 0,1, то консоль выдаст такой результат:
0,30000000000000004
Но постойте, мы ведь точно знаем, что 0,1 + 0,2 = 0,3. В чём же дело? Такой странный ответ получился из-за особенностей двоичной арифметики.
Перед тем как сложить числа 0,2 и 0,1, компьютер сначала переводит их в двоичный вид. При этом у некоторых десятичных чисел нет точного значения в двоичной системе счисления. 0,2 и 0,1 — как раз из таких чисел:
- 0,210 = 0,00110011001100…2;
- 0,110 = 0,00011001100110…2.
Так как нет возможности хранить в памяти бесконечное количество цифр, компьютер округляет числа — поэтому при сложении получаются неожиданные результаты.
Этой проблемы можно избежать, если использовать специальные типы данных, которые предназначены специально для десятичных чисел. Например, в Java для этого есть класс BigDecimal. Эти типы данных требуют больше памяти и работают медленнее стандартных типов float и double, но зато результат всегда будет предсказуемым.
Из-за этой особенности банковские приложения вовсе не используют десятичные числа для учёта денег, а хранят все данные в целочисленных копейках. Например, если на счету пользователя лежит 100,6 рублей, то в коде приложения эта сумма будет равна 10 060 копейкам. Благодаря этому пользователи банковского приложения могут быть уверены, что при выполнении арифметических операций содержимое их счёта не округлится в меньшую сторону.
Что нужно знать о действительных числах
Сегодня вы узнали, что такое множество действительных (вещественных) чисел. Повторим изученное:
- Действительные (вещественные) числа — это все целые, натуральные, рациональные и иррациональные числа.
- Ноль — тоже действительное число.
- Термины «действительные числа» и «вещественные числа» — синонимы.
- На координатной прямой находятся все действительные числа.
- Разные множества действительных чисел можно представить в десятичной, целой, дробной или экспоненциальной форме.
- Экспоненциальная форма — это значимая часть, называемая мантиссой, умноженная на основание системы счисления в определённой степени, называемой порядком, где порядок — это показатель сдвига плавающей запятой.
- В памяти компьютера числа хранятся в экспоненциальной двоичной форме. Она состоит из знакового бита, двоичной экспоненты и мантиссы.
- При работе с действительными числами на компьютере будьте аккуратны, чтобы соблюсти точность вычислений.
Комплексные числа — числа вида z = a + bi, где a и b — действительные числа, а i — мнимая единица.
Мантисса — целое число, которое представляет старшие разряды действительного числа.
Порядок — целое число, которое задаёт нужную степень двойки.
